Mr. Rogers - AP Statistics Objectives

Syllabus 1st Quarter 2nd Quarter 3rd Quarter 4th Quarter 1 Distributions 2 N-Distribution 3 Regression 4 NL Regression 5 Data

Unit Plan Practice Test Practice Test Answers

Chapter 12.2: Nonlinear Regression AP Statistics Standards I. Exploring Data: Observing patterns and departures from patterns (continued) D. Exploring bivariate data Transformations to achieve linearity: logarithmic and power transformations

Objectives Essential Question: Is everything we'd like to study and model linear? Chapter 12.2: 2 Variable Data Continued Modeling Exponential Data Explain how data can be transformed so that linear regression produces an exponential function. First: convert all y data points to ln y. On a TI-83 calculator, if y-data is stored in L1 ans x-data is stored in L1, do LN L2 sto L4 Second: do linear regression for L1, L4 Finally: manipulate the data as shown below Time Microbes 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 ln y = ax + b e (ln y) = e[ax + b] y = [ eax ] [ eb ] y = [ eb ] [ eax ] let eb = K y = keax Formative Assessment: perform the transform on the above data and derive an exponential model from it. Compare this with the linear model. Make scatter plots of both transformed and untransformed data. Are the plots concaved upward, concaved downward, or linear? Give examples where an exponential regression model would be appropriate. Growth or decay over a period of time (response variable multiplied by a fixed amount in each time interval) such as: Bacteria population vs. time New technologies often improve at an exponential rate. Example: the doubling of computer power every 2 years (Moore's Law) New industries often go through an exponential growth spurt. Example: Growth in wind power (wind power map) Radioactive decay (decay of a population of atoms) Formative/Summative Assessment: Using the wind power links provided above and the Estimated Energy Use Sankey diagram, predict the % of total energy consumption for the United States that will be provided by wind power 10 years from today. Include your calculations and discuss your conclusions in a one-page writeup. Assume that energy consumption remains at 2012 levels.   Explain how to determine if an exponential model is appropriate. theoretical basis such as objective 2 above random residuals (this means exponential regression is appropriate. It does not necessarily mean it's right.) Note: extrapolation can be especially risky for exponential growth models because given enough time, their output approches infinity. To use them wisely, it's necessary to consider the factors that currently are driving growth and the factors that could eventually limit further growth. Explain why an exponential model should not be selected on the basis of optimizing r-square. A different form of  non-linear equation may have a higher R2 value but be less appropriate. Perform exponential regression on a TI-83 calculator using the NON-transformed data and note that these results and the results obtained with transformed data are mathematically the same. NON-transformed data: y = abx Transformed data:  y = keax y = k(ea)x Note that both k and ea are constants, so we can let: a = k and  b = ea By substitution: y = abx Homefun (formative/summative assessment): Read section 12.2; Exercises 37 p. 788 Relevance: Exponential data is commonplace in many business, biological, chemistry, physics, and other  areas. Knowing how to deal with it and how to model it is a significant career skill.

Essential Question: If a mouse weighing 0.5 lb were scaled up by a factor of 100, how much would it weigh? Modeling Power Function Data Explain how data can be transformed so that linear regression produces a power function. First: convert all x and y data points to ln x and ln y. On a TI-83 calculator, if y-data is stored in L1 and x-data is stored in L1, do LN L1 sto L3 and  LN L2 sto L4 Second: do linear regression for L3, L4 Finally: manipulate the data as shown below. Pumpkin Dia. Surface Area 1 1.2 2 4.7 3 9.0 4 16.9 5 25.1 6 36.5 7 49.0 8 64.9 ln y = a(lnx) + b e (ln y) = e[a(lnx) + b] y = [ e(lnx)a ] [ eb ] y = [ eb ] [ xa ] let eb = K y = kxa Formative Assessment: perform linear regression analysis and find R2. Transform both x and y data. repeat the process. Convert the linear regression equation  to a power model. Give examples where a power regression model would be appropriate. Definition of scaling factor: If an object is to be scaled up to a larger size without changing the appearance of the object, all the dimensions of the object have to be multiplied by a common factor. This factor is called the scaling factor. Scaling problems: Volume & mass scale with the cube of the scaling factor Note that the following volume equations all contain a cubed term. vol of a sphere = 4/3πr3 vol of a cube with side-length of L = L3 Area scales with the square of the scaling factor Note that the following volume equations all contain a squared term. area of a circle = πr2 area of a shere = 4πr2 area of a square with side-length of L = L2 Explain how to determine if a power model is appropriate. theoretical basis such as objective 6 above random residuals Explain why a power model should not be selected on the basis of optimizing r-square. A different form of  non-linear equation may have a higher R2 value but be less appropriate. Perform power regression on a TI-83 calculator using the NON-transformed data and note that these results and the results obtained with transformed data are the same. For more information about scaling and why it's incredibly important Read: Insultingly Stupid Movie Physics Chapter 4, Scaling Problems: Big Bugs and Little People, pp 51 - 66 Relevance: Power-function data is commonplace in many business, biological, chemistry, physics, and other  areas. Knowing how to deal with it and how to model it is a significant career skill.    Homefun (formative/summative assessment): Exercise 39, 43, 45 pp. 789 to 791

Essential Question: Can any type of non-linear data be transformed or liearized? Other Forms of Modeling Non-linear Data Describe how any power function can be linearized if the power or exponent is known. Phenomena Equation Sample Data Dropped object in freefall (negligible air resistance). g = 10 m/s2 y = k t2 Where: y = distance fallen t = time k = a const.   = 1/2 g   = 5 t t2 y 1 5.5 2 19.5 3 50 4 75 5 135 Perfect gas laws n= 1 mole R = 8.3 L(kPa)/(Kmol) T = 273 K v = k p-1 where: v = volume in L p = pressure k = constant   = nRT   = 2270 (L/kPa) p p-1 v 1 2275 2 1133 3 753 4 568 5 453 Period of a swinging pendulum g = 10 m/s2 T = k L1/2 where: T = period L = length k = constant   = 2pg1/2   = 19.9 L L1/2 T 1 20 2 28 3 35 4 40 5 44 Note: when performing regression analysis on the linearized data, the slope of the line equals the constant in the equation. Formative Assessment: perform linear regression analysis and find R2 for the linearized versions of each of the above data sets. Compare the slopes to k for each data set.   Homefun (formative/summative assessment): Exercise 33, 34 p. 786

Essential Question: What is the most common form of extrapolation? Interpreting Correlation and Regression Decry the evils of extrapolation but also be aware that it's commonly used. projected sales-- in order to plan ahead, companies will often attempt to predict the next year's sales and earnings based on regression analysis of data from previous years. projected population growth projected impact of advertising dollars spent -- used for determining what the future advertising budget should be. radioactive dating -- there's sound theory backing radioactive dating but obviously no one collected data on it thousands of years ago. Formative Assessment: Explain why real growth curves are always sigmoidal shaped (s-shaped).   Evaluate the degree of risk associated with extrapolation. The risks associated with extrapolation are moderated by the following: Sound theoretical basis for the regression model Strong supporting data from independent sources.For example: a limited amount of extrapolation using the recent exponential grow in American wind-power electrical generation is reasonable based on ready availability of wind resources, low cost compared to other forms of generation, and concerns about global warming, 3 factors which make wind-power attractive. Extrapolating only slightly beyond the range of the actual data. The greater the distance beyond the data's range, the greater the risk. Simple regression model such as linear, exponential, or power. Extrapolation with high order polynomials is very dangerous (see example). Positive results with various indicators such as outlier-free scatter plot, high r-square, random residuals, etc. Identify possible lurking variable. An important variable which is not included in the study. Name the most common lurking variable. time State the pitfall of using averaged data in regression models. It makes the r-squared value higher. Hence, the results look better than they really are.

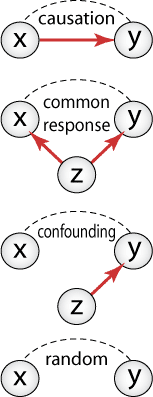
Essential Question: Can we ever be completely sure that causation exists? Causation In other words, is the association between the x and y variables due to  the x-variable actually causing a response in the y-variable. State 4 possible explanations for getting a strong association based on regression/correlation analysis. Causation --Sometimes it's true: x causes y Common response variables (affect both x & y variables), example: rum (y) and Methodist Ministers (x) are both affected by the common response variable, population growth (z). Confounding variables (affect the y variable but not the x), example: The shaman chants an incantation (x) and five days later the patient who seemed near death gets well. The patient's immune system (z) was the real cause. Random chance (the association is temporary in nature and is the result of numerous unidentifiable factors that are not reproducible), example: Bob finds a 1957 penny on the sidewalk as he enters the casino. When he subsequently wins $2000 dollars at roulette, he concludes that the penny is his good luck charm. The dog barked and the tree fell down. Formative Assessment: answer the following questions: Did the dog cause the tree to fall? Are there possible common response variables? Are there possible confounding variables? Could the two events coincide due to random events? Could the tree-felling dog be tested in an experiment? Is there a plausible theory for why the tree could be felled by the noise of a dog barking?   Explain 4 steps toward establishing causation. Generally all 4 steps are required especially for controversial situations. Carefully controlled experiments -- the gold standard. Can sometimes be as simple as turning the causative variable on and off. Weakness = experiments often are run in an artificial environment. Multiple independent observational studies of different types Account for, control, or eliminate lurking variables -- Must be done in both observational and experimental studies. Accounting for lurking variables usually means including them in multiple linear regression analysis. Develop a plausible theory -- without a plausible theory, even experimental data can be questioned. Summative Assessment: Test objectives 1-18