Mr. Rogers - AP Statistics Objectives

Syllabus 1st Quarter 2nd Quarter 3rd Quarter 4th Quarter 1 Distributions 2 N-Distribution 3 Regression 4 NL Regression 5 Data

Unit Plan Practice Test

Chapter 1: The Normal Distribution AP Statistics Standards I. Exploring Data:  (continued). II. Anticipating Patterns: C. The normal distribution Properties of the normal distribution Using tables of the normal distribution The normal distribution as a model for measurements

Objectives Essential Question: What does it mean to be in the 95 percentile group? Ogives Understand the meaning of percentile. Example: if a score of 57 is at the 10th percentile then 10% of the observations or data points fall below a score of 57. Convert distribution data in various forms into a relative cumulative frequency graph (generally expressed in %), often called an ogive. Note: Ogives are often drawn with the otherwise abhorrent connect the dots style. Ogives tend to have a sigmoidal shape. Formative Assessment: create ogives out of the following items or the following items out of ogives. data table 5-number summary stem and leaf plot histogram   Homefun (formative/summative assessment): prob. 1,3,5,9 pp.105-106     Essential Question: What will changing the units of measurement do to measures of spread and central tendency? Linear Transforms What is a linear transform? (See p. 53). xnew = a + b∙xold Example: the linear transform to change from Celsius to Fahrenheit (ºF) = 32 + 1.8 (ºC)   State the effect that multiplying each number by a constant and/or adding a constant to each number in a data set has on the following: (This effect is important to know when changing the data points' units.)   (each data point) + a (each data point) * b mean (mean) + a (mean) * b median (median) + a (median) * b standard deviation no change (std dev) * b IQR no change (IQR) * b range no change (range) * b Q1 and Q3 (Q1) + a & (Q3) + a (Q1) * b & (Q3) * b Formative assessment: Using the TI-83 calculators and monthly temperature data in Fahrenheit from the Geenville-Spartenburg Airport, calculate and record the mean, median, standard deviation, IQR, range, Q1, and Q3 for both Fahrenheit and Celsius. Convert the recorded Fahrenheit values directly to Celsius. How do the converted values compare to the ones calculated in Celsius.? Homefun (formative/summative assessment): prob. 19, 21 p. 107 Essential Question: Is the bell-curve real? The Normal Distribution Define density curve. Models a distribution Above horizontal axis Area under it = 1 Area under part of the curve = probability mean: the "balance point", similar to the center of mass in physics. median: the equal area point Describe the normal distribution. Symmetrical Bell Shaped Range negative infinity to positive infinity How to Calculate the Normal Distribution pdf = 1/[σ(2π)] • exp[ - (x - μ)2 / (2σ2)] Where: pdf = probability density function (height or y-axis coordinate of the N-distribution) x = horizontal axis coordinate μ = mean σ = the standard deviation Note: determining the shape of the normal distribution requires a knowledge of both the mean and standard deviations   Create or analyze drawings of normal distributions by knowing where where the 2 inflection points occur. An inflection point is the point on a curve where the curve changes from concaved upward to concaved downward For N-distr. inflection pts = ± 1 sigma from the mean) State the probability of getting a data point with a specific value. zero. Why? A point has a width of zero, hence, there's zero area under a single point on the normal distribution Correctly use and interpret N (mean, sigma) notation. The mean and standard deviation -- just 2 numbers -- completely describes a normal distribution. Incredibly, just these 2 numbers have the power to characterize massive sets of data points with a diversity of values. Evaluate the effects on a normal distribution of increasing or decreasing the standard deviation. Relevance: The normal distribution is ubiquitous. Discussions about it pop up in all kinds of both technical, news, and popular publications. Homefun (formative/summative assessment): prob. 27, 29, 31, 33 pp. 108 - 109

Essential Question: How is the area under the bell-curve related to the standard deviation? Estimating Areas Under Normal Distributions Find probabilities (areas under the curve) using the 68-95-99.7 Rule for normal distributions (sometimes called the empirical rule). Note: in the 1st part of the test for this chapter, you will not be permitted to use calculators or tables. The entire test will be based on the above rule. Formative assessment: Using the empirical rule evaluate areas under the curve. Relevance: If you know the empirical rule you can easily double check your answers when solving for areas under the n-distribution. The ability to evaluate answers is a very high level skill.  Homefun (formative/summative assessment): prob. 43, 45 p.131

Essential Question: Does an ogive give the same information as a normal distribution? Relating the Normal Distribution to Ogives Convert the N-distribution into an ogive (cumulative frequency plot) using the empirical rule. (Formative assessment, group work) Normal Distribution, Wikipedia http://en.wikipedia.org/wiki/Normal_distribution, 9-8-2008 Estimate the mean, median, sigma, Q1, Q3, and IQR using an ogive for a normal distribution. (Formative assessment, group work)

Essential Question: How different are the characteristics of non-normal distributions to normal distributions? Non-Normal vs. Normal Distributions Estimate the median, quartiles, and probabilities for any distribution by estimating the area under the curve: Uniform Triangular Skewed Be as one with the 0-75-89 Rule based on Chebyshev's Theorem, which applies to any distribution. Tail areas, several standard deviations from the mean, of the normal distribution are often used in decision making. Chebyshev's Theorem indicates the maximum error in calculating a tail area if a distribution is incorrectly identified as a normal distribution. Chebyshev's Theorem: p = (1 - 1/k2) Where: p = the lowest possible probability of finding a value between  ±k standard deviations from the mean. Formative Assessment: Calculate the maximum error in tail areas beyond ± 1, 2, and 3 sigma that can be caused by assuming a distribution is normally distributed when it isn't. From the above, mathematically evaluate why Chebyshev's theorem only has value for making predictions when K > 1.

Essential Question: How can the area under the bell-curve be determined more accurately than by estimating? Determining Areas Under the Normal Distribution By Using Tables Derive the mathematical definition of a z-score (abbreviated as z) using its English language definition and use it for calculate z-scores. z-score = number of standard deviations from the mean Find areas under the normal distribution using tables. Note, the tables contain a "standardized normal distribution". Here, the mean = zero and the standard deviation = 1. Probability = area under curve Formative Assessment: Find the area under the curve of the normal distribution by using tables. Essential Question: How does the box and whiskers plot look like for normally distributed data? Working Area Under the Curve Problems Backwards Find z-scores corresponding to LL, Q1, median, Q3, UL of a modified box and whiskers plot for normally distributed data. Formative Assessment: Draw a box and whiskers plot of a normal distribution. Using a normal distribution, estimate a critical value given the probability of finding a value as extreme or more extreme (a tail area). 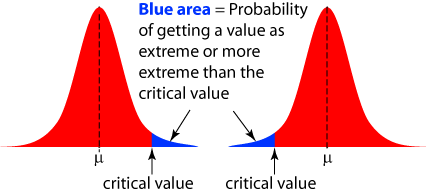Homefun (formative/summative assessment): prob. 47, 49, 51, 55 p.132

Essential Question: How can we tell if a distribution is normal and why would we care? Evaluating Normality Evaluate the normality of a distribution by examining histograms, stem plots, dot plots, ogives, or box and whiskers plots.   Bell shaped Sym-metrical Follows 68-95-99.7 Rule whisker ≈ 1.5 x ( box width) histograms, stem plots, dot plots x x x   ogives   x x   box & whiskers plots.   x   x Formative Assessment: Evaluate various data sets to determine if it is reasonable to assume that they are normally distributed.   Evaluate the normality of a distribution using a normal quantile plot on a TI-83. n-distributions look like straight lines on normal quantile plots. Homefun (formative/summative assessment): prob. 65, 67, 69, 75, 71 pp. 134 - 135 Essential Question: What is the best way to find probabilities associated with normal distributions? Work quality control reject rate problems. Note: rejects occur in the tail areas. Find areas under the normal distribution using tables using a TI -83 calculator. normalcdf (L,U,M,S) Have you taken your LUMS today? Lower value Upper value Mean Standard deviation Given a tail area, find the critical value (see objective 15) using a TI-83 calculator. invNorm (A,M,S) I think therefore I AMS. Area (must be a decimal fraction) Mean Standard deviation Remember, in tables for finding standard normal distribution probabilities, the mean = zero and the standard deviation = 1. If these values are input into invNorm along with an area, the result will be a z-score. Homefun (formative/summative assessment): Work the Chapter 2 practice Test T2.1 to T2.13 138-139   Essential Question: How can I make an "A" on the test? Normal Distributions Review Work the practice test. Review the objectives. Look over free response problems from previous years. Master the vocabulary (see example below). Summative Assessment: Test--Objectives 1-24