Mr. Rogers - AP Statistics Objectives

Syllabus	1st Quarter	2nd Quarter	3rd Quarter	4th Quarter
11 t-Test	12 Inf for Prop	13 Chi Test	14 Regression HT

Unit Plan Practice Test

Latin/Greek Root Words arch--------->ancient, example: archtype;         chrono------>time, example: chronology;             -dom----------->quantity/state, example: freedom               fer-------->carry, example: transfer;               gen--------->birth, example: generate;                 luc-------->light, example lucid;                 neo--------->new, example: neonatologist;                olig--------->few, example: oligarchy;              omni--------->all, omniscient;            sym--------->together, symbol; (Statistics connection)

AP Statistics Standards IV. Statistical Inference: Confirming models and testing hypotheses (30% –40%) B. Tests of significance C. Special case of normally distributed data  t-distribution Single sample t procedures Two sample (independent and matched pairs) t procedures

Objectives   Essential Question: How does the US justice system compare to statistical analysis?   Hypothesis or Significance Testing State the question asked by a significance test and the two possible answers. Is there clear evidence of an effect? State a generic null hypothesis. There is no clear evidence of an effect. There is nothing new or out of the ordinary. The status quo exists. State a generic alternative hypothesis. There is clear evidence of an effect. Give the null and alternative hypothesis for the American justice system. Null Hypothesis: not guilty. This is the status quo for most people. Alternative Hypothesis: guilty Define P-value. Assuming Ho is true, the probability of obtaining a test statistic as extreme or more extreme than the one obtained is ______. The smaller the p-value, the stronger the evidence is against Ho State the statistic used for indicating the level of significance. (Hint: it begins with a "p".) State the type of distribution used for tests of significance. The sampling distribution. Describe one tail and two tail tests from the standpoint of the null hypothesis and the p-values. Be as one with "z-test for a population mean". Perform "z-test for a population mean" in the following ways: by hand (using the calculator only for basic mathematics) using z-tables. by hand, using the calculator only for basic mathematics and finding areas using the hypothesis testing features of the TI-83 using Minitab software Homefun (formative/summative assessment):  Exercise 1, 5, 7, 9, 15, 17 pp. 546 to 547   Essential Question: Can a statistically significant hypothesis have no practical value? Alpha Levels Define the significance level, alpha--predetermined maximum acceptable p-value for rejecting the null hypothesis. Use one and two tailed tests of significance. one-tailed: area of tail = alpha two-tailed: area of each tail = (alpha) / 2   Use alpha to evaluate statistical significance. 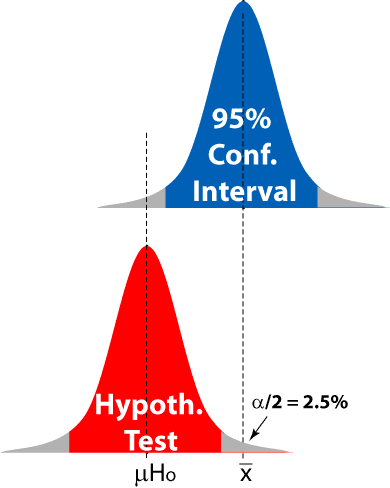Use a confidence interval (confidence level = C) as a significance or hypothesis test. significance level = (1 - C) a confidence interval is essentially identical to a 2-tail hypothesis test. Formative Assessment: What two types of statistical tools are used for inference and what type of distribution is used for making inferences?   Describe the difference between statistical and practical significance. Even a tiny difference between x-bar of a sample and a population will be statistically significant if the sample size is large enough. Such a tiny difference may have no practical significance. State when statistical inference is not valid. (When based on data from a poorly designed study or experiment.) Homefun (formative/summative assessment):  Essential Question: How many ways can you make an error of judgement? Types of Errors Pass the ultimate test of true statistics nerdhood: Explain the difference between type 1 and type 2 errors. Explain what a type 1 and type 2 error is for the American justice system. Ho: innocent, Ha: guilty type I error: punish an innocent person type 2 error: let a guilty person go free Explain what a type 1 and type 2 error is for quality control in manufacturing. Ho: the product is acceptable to the customer Ha: the product is unacceptable to the customer type I error: reject acceptable product and don't ship it. type 2 error: ship unacceptable product to the customer Generate a truth table for a hypothesis test. State how alpha relates to the type 1 error. Whether a one or two tailed test, alpha always = type 1 error. Name the hypothesis which is considered true when determining the probability of having a type 1 error. Ho Name the hypothesis which is considered true when determining the probability of having having a type 2 error. Ha Identify the areas representing the probabilities of type 2 and type 1 errors on a diagram of a hypothesis test showing a hypothetical sampling distribution. Determine alpha and beta. beta = type 2 error Power given: β = (1 - power)   Special Cases for β = Type 2 Error μHa = μHo: β  = (1 - α) μHa = (α boundary): β  = 50%   Determine the power of a hypothesis test. power = (1 - β) Beta given: power = (1 - β)   Special Cases for Power μHa = μHo: power = α μHa = (α boundary): power = 50%   Plot and interpret a power curve (power vs. separation between μHo and μHa) for a hypothesis test. sigmoidal shape at zero separation power =  alpha asymptote at 100% (as separation approaches infinity, power approaches 100%) State how power can be applied to quality testing in manufacturing.   Homefun (formative/summative assessment):  Exercise 21, 23, 25, 27, 29 pp. 548 to 549 Summative Assessment: Test Objectives 1-27   Essential Question: How does a confidence interval for proportions compare to one for means? Ch. 12.1 Inference for Proportions State the meaning of p-hat. A statistic estimating a population proportion p-hat =    count of successes in sample   count of observations in sample Calculate the mean and standard deviation of a binomial distribution. Data Type Mean Std Dev count or number np [np(1 - p)]^0.5 proportion p [p(1 - p) / n]^0.5 Be aware that a binomial distribution (the distribution typically used for analyzing proportions) is essentially a sampling distribution. Note that as a sampling distribution, when the sample size is large enough (see below), the distribution begins to resemble a normal distribution. When appropriate, correctly model a binomial distribution as a normal distribution if the 2 conditions shown below are met. np ≥ 10 n(1-p) ≥ 10   Perform a hypothesis test comparing a single large sample proportion (p-hat) against a know population proportion (p). Note, this is a one proportion z-test. Z =   (p-hat) - p [p(1-p)/n]0.05   Homefun (formative/summative assessment): Exercise 35, 39, 41, 43, 47, 57, 59 pp. 562 to 565   Essential Question: How can we perform significance tests with small samples and an unknown standard deviation for the population? Estimating a Population Mean When Its Standard Deviation is Unknown State the 2 assumptions that need to be met for using a t-test. SRS Normal Distribution of the population (symmetrical with single peak) Calculate standard error of a t-statistic SE = s / ( n^.5 ) . If the sample size is large, the z-interval can be used with the above SE. Explain when a t statistic is used rather than a z-score. Population Standard deviation not known Sample Size is Small Calculate t statistics. State the degrees of freedom for a one-sample t-test. df = ( n-1 )   Perform one sample t-procedures: by hand (using the calculator only for basic mathematics) using t-tables. by hand, using the calculator only for basic mathematics and finding areas. tcdf (L,U,D) Lower t-value Upper t- value Degrees of Freedom using the hypothesis testing features of the TI-83. Note that μ is the mean associated with Ha μo is the mean associated with Ho using Minitab software Use the t-distribution with the following limitations: Sample Size Skew Nearly N-Distr Outliers Less than 15 None Yes No At least 15 Minor Yes, minor skew ok No At least 30 Significant Yes, skew ok No   Homefun (formative/summative assessment):

Essential Question: What is the single most powerful form of hypothesis testing and why? Matched Pairs Testing (Spanish Camp) Apply the t-test of significance to matched pairs (MP) situations. MP tests are 1 sample t-tests Ho: μ = 0 df = (number of pairs - 1) Be aware: you must establish that the population is approximately normally distributed. How to Establish That a Population is Normally Distributed Box Plot - symmetrical, box width smaller than a whisker's width Normal Quantile Plot - straight line Explain what is meant by a robust test or confidence interval. p-value  or confidence interval changes little if assumptions are violated. Be as one with the information in the "using t procedures" box on p.. Be aware that outliers are very harmful to the t-test. Making a modified box plot of the data in order to look for outliers is a very good idea.     Homefun (formative/summative assessment): Exercise 65, 67, 73, 75, 77 pp. 587 to 589; Work the entire AP Statistics Practice Test pp. 597 to 599

Essential Question: How can you determine if 2 populations differ if at the start you have no information? Two-Sample t-Test State the assumptions made for two-sample tests. (p. 650) SRS used for generating the sample independent - matched pairs violate independence normally distributed population Create confidence intervals and hypothesis test using two sample t procedures assuming that the sigmas of the two populations are unequal. This is the most conservative assumption. Ho: μ1 - μ2 = 0  but can also be written, Ho: μ1 = μ2   Test Statistic for  Hypothesis Testing Margin of Error for Confidence Interval t = (xbar1 - xbar2) - 0 (s12/n1 + s22/n2)0.5 ME = t* (s12/n1 + s22/n2) 0.5 Create confidence intervals and hypothesis test using two sample t procedures and the most conservative method of determining df. df = (the lower of n1 -1 or n2 - 1) Be aware of the more accurate way to calculate df as is done by the TI-83 calculator. This method can return a df that includes a decimal fraction. For example: df = 12.37 Perform two sample hypothesis t-procedures on the TI-83. State the key assumption required for using the pooled two-sample t-procedures. This is the method is an option in the TI-83 calculator. The sigmas of the two populations are the same   Homefun (formative/summative assessment): Exercise