Mr. Rogers - AP Statistics Objectives

Syllabus	1st Quarter	2nd Quarter	3rd Quarter	4th Quarter
Probability	Binomal Distr	Sampling Distr	Conf Intervals	1st Sem Exam

Unit Plan Practice Test

Latin/Greek Root Words arch--------->ancient, example: archtype;         chrono------>time, example: chronology;             -dom----------->quantity/state, example: freedom               fer-------->carry, example: transfer;               gen--------->birth, example: generate;                 luc-------->light, example lucid;                 neo--------->new, example: neonatologist;                olig--------->few, example: oligarchy;              omni--------->all, omniscient;            sym--------->together, symbol; (Statistics connection)

Chapters 8: Estimating With Confidence AP Statistics Standards IV. Statistical Inference: Estimating population parameters and testing hypotheses (30% –40%) Statistical inference guides the selection of appropriate models. A. Estimation (point estimators and confidence intervals) Estimating population parameters and margins of error Properties of point estimators, including unbiasedness and variability Logic of confidence intervals, meaning of confidence level and confidence intervals, and properties of confidence intervals Large sample confidence interval for a proportion Large sample confidence interval for a difference between two proportions Confidence interval for a mean Confidence interval for a difference between two means (unpaired and paired)

Objectives Essential Question: Is there a way to get any researcher in the world to agree agree that your conclusions are reasonable even if they disagree with them? Statistical Inference Correctly use the term statistical inference. To draw a conclusion from data in a formal manner using well defined procedures Give the mathematical and a quick and dirty explanation of a confidence interval. Conf. Int. = estimate ± (margin of error) An estimate of a parameter based on a statistic, with a means of accounting for sampling variability. Relevance: Confidence intervals are a primary means of communicating statistics in all areas of science, social science, political science and engineering.. Homefun (formative/summative assessment):  -- Read section 8.1

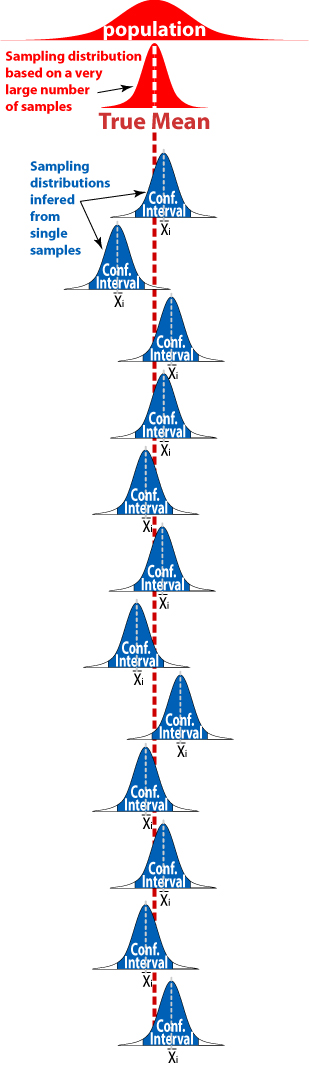
Stats Investigation: Estimating a Proportion Purpose: Determine a reasonable way to estimate a proportion for a population. Instructions: Write a rational hypothesis for what the proportion of red cards is in a deck of cards. Draw 10 samples with n=2 and 10 samples with n=20 from a deck of cards. Remove a card one at a time. Replace and shuffle the deck each time a card is drawn. Do this twice for each sample of two and twenty times for each sample of 20. Record the the proportion of red cards for each sample.  Create an interval around each sample which you feel has a high chance of containing the mean. Record your reasons for making the interval. Make two plots of all the intervals. One for n=2 and one for n=20. The plots should look like the one on page 511 minus the normal distribution picture.  Repeat the process for a second deck of cards. Questions /Conclusions: Which sample size tended to have the widest interval? Did every interval contain the true mean?

Essential Question: How can you express a measurement in an internationally accepted manner? Confidence Intervals   State the 3 parts of a confidence interval and explain their meaning.  Confidence level the fraction or percentage of conf. intervals that will contain the parameter in a large number of trials (see drawing at right) Estimate the statistic used to estimate a parameter, often a sample mean Margin of error 2*(ME) = (width of conf. int )   State the type of distribution which confidence intervals (CIs) are based on and explain what characteristic makes it so useful.CIs are based on sampling distribution, which given a large enough sample size, tend to be normally distributed. This is a great advantage because the mathematics of normal distributions are well defined. Sketch the appropriate picture of a confidence interval. A confidence interval is always represented as a symetrical center section of a normal distribution representing the sampling distribution. See the blue distributions shown at right. Calculate margin of error when standard deviation is known. ME = z* [σp / (n)0.5] Describe what happens to the margin of error as confidence level (C) is increased. ME approaches infinity as C approaches 100% ME approaches zero as C approaches 0%   Formally state the meaning of a level C confidence interval. If a study were repeated numerous times, C represents the expected % of the resulting confidence intervals that would contain the true parameter. Tell why the margin of error is not a measure of accuracy in the data. The accuracy of a estimate is typically unknown. (Remember, we would have to know the true parameter to determine the accuracy of the estimate because accuracy is a measure of how close an extimate comes to the true parameter.) ME depends on an arbitrarily determined value of C. (C usually = 95% but this is a convention not a mathematically derived principle Given that margin of error is not a measure of accuracy or "error," State what it really represents. (Expected sampling variability) Be as one with the cautions. Homefun (formative/summative assessment): Exercise 5, 9, 17, 21, 23, 25, pp. 480 to 484     Essential Question: How does a confidence interval for proportions compare to one for means? Inference for Proportions State the meaning of p and p̂, p-hat. State the standard deviation of the sampling distribution (SD) σp̂ = [ p (1 - p ) / n ]0.5   Create a large sample confidence level for a proportion. Since p is not known p̂ must be used instead for calculating standard error, an estimate of the standard deviation of the sampling distribution. Confidence Interval = p̂ ± z* [ p̂ (1 - p̂ ) / n ]0.5 Requirements: Normally Distributed SD: np >= 10 and n(1 - p) >= 10 Population Size >= 10n Given a target value for the maximum acceptable margin of error, calculate the minimum sample size.Hint: When the true proportion is not known always use p̂ = 0.5 or 50%. This give the most conservative value for n when solving for n using the following equation: ME = z* [ p̂ (1 - p̂ ) / n ]0.5   Homefun (formative/summative assessment):  Read section 8.2 -- Exercises 29, 35, 39, 41, 43, 45, 51, pp. 496 - 498     Essential Question: How can we account for the greater uncertainty of analyzing data when sample size is small and little is known about the population?   Estimating a Population Mean When Its Standard Deviation is Unknown State the 2 assumptions for drawing inferences about a population mean when sigma is not known. SRS Normal Distribution of the population (symmetrical with single peak) Calculate standard error of a statistic SE = s / ( n^.5 ) . If the sample size is large, the z-interval can be used with the above SE. Explain when a t statistic is used rather than a z-score. Population Standard deviation not known Sample Size is Small Calculate t statistics. State the degrees of freedom for a one-sample t-test. df = ( n-1 ) Construct confidence intervals using the t statistic. ME = t* s / ( n0.5 ) Perform one sample t-procedures: by hand (using the calculator only for basic mathematics) using t-tables. by hand, using the calculator only for basic mathematics and finding areas. tcdf (L,U,D) Lower t-value Upper t- value Degrees of Freedom using the hypothesis testing features of the TI-83. Note that μ is the mean associated with Ha μo is the mean associated with Ho using Minitab software Use the t-distribution with the following limitations: Sample Size Skew Nearly N-Distr Outliers Less than 15 None Yes No At least 15 Minor Yes, minor skew ok No At least 30 Significant Yes, skew ok No   Homefun (formative/summative assessment):  Read section 8.3, Do Exercises 55, 59, 63, 69, 75, 77 Essential Question: How can I make an "A" on the test? Confidence Interval Review Master the vocabulary Work the practice test. Review the objectives.   Summative Assessment: Unit Exam objectives 1 - 24

Stats Investigation 8.2: Margin of Error Purpose: Determine the effects that  changes in confidence level, sample size, and standard deviation have on margin of error. Instructions: You will make three different plots as follows: Margin of error vs confidence level with sigma = 1 and n = 100. Vary confidence level from 60% to 99%.  Margin of error vs sigma with confidence level = 95%, and n = 100. Vary sigma from 1 to 5.  Margin of error vs sample size with confidence level = 95% and sigma = 1. Vary n from 100 to 500.  Questions /Conclusions: What is the effect of doubling the sigma and why? What is the effect of doubling the sample size and why? What is the effect of increasing the confidence level from 90% to 95%? Of the three items mentioned above, which one(s) are under the control of the experimenter? What type of error does the margin of error represent? Why is margin of error not a measure of accuracy? What sampling technique must be used if valid confidence intervals are calculated? Is a high confidence level necessarily more meaningful than a low confidence level?