|
|
|
|
|
Essential Question:
Would a rail-gun have recoil? |
Momentum and Collisions
-
Define momentum 2 ways.
- How hard it is to stop an object
- P ≡ mv
- State Newton's second law in terms of
momentum.
S F = dP / dt
- Name two types of situations where momentum is
conserved.
- Explosions -
things flying apart
-
Collisions
- things flying together
- State one of the key reasons momentum can be conserved.
-
It's a vector!
- Solve 1 dimensional "explosion" problems using
conservation of momentum.
- Describe the difference between elastic and
inelastic collisions.
|
Collision Type |
Conservation Momentum |
Conservation Energy |
Conservation Kinetic En. |
Particles Stick |
| Elastic |
Yes |
Yes |
Yes |
No |
| Inelastic |
Yes |
Yes |
No |
Yes |
- Solve 1 dimensional inelastic collision
problems using conservation of momentum.
Homefun: Read 9.1 & 9.3,
Questions 1-10 p. 281; Problems 1, 3, 5, 19.
Homefun: Questions 1 - 11
p.44-45; prob 1, 3, 5, 7, 9
-
 Read:
Insultingly Stupid Movie Physics Read:
Insultingly Stupid Movie Physics
- Chapter 7, Movie Momentum: The
Attractive Force of Glass, Rail-Gun Recoil, and Cosmic Toyotas, pp 99 - 115
Metacognition Problem Solving Question 9.1:
Do objects collide or fly apart in the problem?
If they do then the problem can often be solved using conservation of momentum.
Solutions for final velocity of an object in one dimensional momentum problems
usually end up with a mass ratio time the starting velocity.
|
|
|
|
|
Lesson 1
Key Concept: Conservation
of momentum
Purpose:
Understand how to use conservation of momentum in problem solving.
Interactive Discussion:
Objective 1 - 4. Note that momentum is one of the great conservation
laws of physics.
Demo
9.1: Objective
3b. Explain that the spheres-on-a-rod will exhibit conservation of
momentum when dropped. On the way down the total mass is the
combined mass of the spheres. On the way up, only the small sphere
will rise. Guess what happens to its velocity?
Video Clip:
Show a video clip of the rail gun scene in Eraser.
In Class Problem Solving:
Objective 5
- Arnie fires the rail gun.
- Bubba pushes Nancy.
Demo
9.2: Objective
6. Demonstrate the difference between elastic and inelastic
collisions using happy and sad spheres.
In Class Problem Solving:
Objective 5
- A moving train car collides with a stationary
car.
- Two meteors with different velocities collide
and fuse.
Resources/Materials: spheres-on-a-rod,
happy and sad spheres |
|
|
Essential Question:
Why is it essential that
collisions between molecules of air be elastic ? |
- Elastic Collisions
- Relevance: Elastic collisions
are useful for analyzing numerous problems from gas dynamics (collisions
between molecules) to billiards.
-
Describe in qualitative terms what happens in one
dimensional elastic collisions.
-
Solve 1 dimensional elastic collision problems.
-
Solve problems inelastic collisions in 2 dimensions.
-
 Solve problems involving elastic collisions in 2 dimensions. Solve problems involving elastic collisions in 2 dimensions.
When a mass collides with a stationary mass of the same size in a glancing
elastic collision, the velocity vectors form a 90 degree angle
afterwards.(p.270)
Metacognition Problem Solving Question 9.2:
Can I break the vectors into components?
The most complex vector problem can always be broken up into simpler 1
dimensional problems. Hence,
The sum of momentums in each dimension after a collision has to be the
same as the sum of momentums in the same dimension before the collision.
-
Think components!
Homefun: prob.15, 19, 21,
33, 37
|
|
Lesson 2
Key Concept: Conservation of Momentum With Elastic Collisions and in
Two Dimensions.
Purpose: Expand
the understanding of how conservation of momentum can be used for
problem solving.
Demo
9.3: Objective
9. Demonstrate elastic collisions on an air track with
combinations of various sized cars.
In Class Problem Solving:
Objectives 9
- Derive an expression for the final velocities
after the elastic collision of equal mass objects in one
dimension.
Interactive Discussion:
Objective 10 - 11.
In Class Problem Solving:
Objectives 10 -11
- When Bob meets Jane at an intersection
- Bouncing billiard balls go boink.
Resources/Materials: Air
track. |
|
|
Essential Question:
Why is the conservation of kinetic
energy for elastic collisions different from conservation of energy? |
Impulse Section 9.2
-
Solve combined conservation of energy and momentum problems
for inelastic collisions.
-
Solve combined conservation of energy and momentum problems
for collisions involving springs.
-
Define impulse mathematically 2 different ways and explain in
general terms what it indicates.
- (imp) = ∫
F(t)
∙ dt
- (imp) = ΔP
- Roughly speaking:
an indication of how
much effect a force will have on changing an object's momentum.
Note:
impulse is a vector.
Metacognition Problem Solving Principle 9.3: Remember
that impulse obeys Newton's third law! In other words, during a
collision, the change in momentum caused by the impulse one object exerts on a
second is exactly the same as the change in momentum caused by the impulse the
second object exerts on the first.
Homefun: Read 9.2, prob. 6, 27, 57, 61
|
|
Lesson 3
Key Concept: Impulse
Purpose:
Understand what happens during a collision.
Interactive
Discussion:
Objective 12. How much force can I take?
In Class Problem Solving:
Objectives 12
-
Ballistic pendulum.
-
Bob and Jane play
chicken with bumper cars (collisions with springs).
-
Bozo burns the rope
on the bozomobile (releasing springs).
Interactive
Discussion:
Objective 13 . How much force can I take?
Demo
9.4: Objective
12, 13. Demonstrate the effects of elastic and inelastic collisions
on a block of wood using happy and sad sphere pendulums. Which has
the higher impulse?
In Class Problem Solving:
Objectives 9
Resources/Materials: Happy
and sad sphere pendulums.
|
|
|
Essential Question:
Why is center of mass important to
martial artists, dancers, and acrobats? |
Center of Mass Section 9.6
-
Define center of mass
|
Discrete objects |
|
|
|
General case |
Xcm =
1/m ∫
X
∙
dm |
Ycm =
1/m ∫ Y∙
dm |
|
English |
the average spatial location of
an object's mass |
-
Find the center of mass of various objects.
-
State whether an object will rotate, translate, or both by
looking at the location of forces relative to the center of mass.
-
Explain how center of mass relates to the stability of
an object.
-
State what happens to the center of mass of an object if it
exploded in outer space.
Metacognition Problem Solving Principle 9.4:
After calculating the center of mass coordinates for an object, does it look
like the object could be balanced by placing a thin support under the center of
mass? Center
of mass is like a balance point. By thinking of it in this manner, it's often
possible to judge if a center of mass calculation makes sense by asking if the
object would balance if suspended from
Homefun: Read 9.4 thru 9.6, prob. 39,
41
|
|
Lesson 4
Key Concept: Center of mass
Purpose:
Calculate the center of mass and use it as a problem solving concept
in momentum problems.
Interactive
Discussion:
Objective 15. All of an object's mass can be considered to exist at
it's center. How can the center of mass be found experimentally?
Demo
9.4: Objective
16. Throwing a meter stick. Throw a meter stick so that it rotates
and so that it translates. What is the difference in how the force
is applied?
Demo
9.5: Objective
16. Attempting to stand on one leg. Stand with the feet spread apart
shoulder width. Attempt to raise one foot and stand on only one foot
without changing the position of your center of mass. (It can't be
done)
Demo
9.5: Objective
16. Throwing an opponent who attempts to punch you (Aikido). Have a
subject stand on one foot with the back leg extended backwards and
extend his fist as far forward possible. This simulates the act of
rushing forward while throwing punch. Have a second person very
lightly pull forward on the wrist of the first person's extended
arm. (This will very easily unbalance the first person. If the
first person were actually rushing forward while throwing a powerful
punch, he would be violently thrown to the ground with both
translational and rotational motion)
In Class Problem Solving:
Objectives
|
|
|
Essential Question:
Why was the Apollo Rocket so huge? |
Rockets and Explosions Section 9.6
Relevance: Want to
learn rocket science? Here it is. Conservation of momentum is the basis
principle that makes rockets go.
-
State what happens to the center of mass of an object when the
parts of an object are pulled together by an internal force (assuming no
external resistance forces).
-
State what happens to the center of mass of a rocket
(including its fuel) when it is accelerating in outer space.
-
Calculate the thrust produced by a rocket.
FT = vm dm/dt
-
State two reasons why a rocket must have a very large supply
of fuel in order to move from the surface of Earth into outer space.
Metacognition Problem Solving Principle 9.4:
Remember that the location of an object's center of mass of a system is only affected by external
forces. Any form of explosion in an unrestrained object will generate internal forces.
Homefun: Read section 9.7,
prob. 43, 51
|
|
Lesson 5
Key Concept: Propulsion using momentum and center of mass
Purpose:
Understand how rockets work.
Interactive
Discussion:
Objective 15.
Demo
9.4: Robot
which propels itself by changing the location of its center of mass.
In Class Problem Solving:
Tsiolkovsky's rocket equation,
or ideal rocket equation is named after
Konstantin Tsiolkovsky who independently derived it and published
in his 1903 work,[
-

where:
- m0
is the initial total mass, including propellant, in kg (or lb)
- m1
is the final total mass in kg (or lb)
- ve
is the effective exhaust velocity in m/s or (ft/s)
-
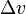 is the delta-v in m/s (or ft/s)
is the delta-v in m/s (or ft/s)
Some typical values of the exhaust gas velocity
Ve for rocket engines burning various
propellants are:
|
|
|
Formal Lab Investigation |
| Title |
Investigation of a Collision on an Air Track |
| Category |
Linear momentum |
| Purpose |
Determine if conservation of momentum can be observed in the
collision of 2 sliders on an air track |
| Models |
∑Pbefore =
∑Pafter conservation of linear
momentum |
| Overview |
Momentum is conserved in a collision as long as there is not a
friction force acting on the objects in a way that significantly
reduces the velocities. Since an air track simulates a friction free
environment, it should be an ideal test platform for conservation of
momentum investigations. Level the air track so that the sliders
remain stationary unless they are pushed.
Place 2 sliders of equal mass on the track. Just before the
collision, the one in back will be sliding toward the stationary one
in front.
Set up a pair of photogates so that the first measures the moving
slider's velocity just before the collision and the second measures
the velocity of the 2nd cart just after the collision.
Gently push the slider in back, measure the results of the
collision, and determine if conservation of momentum is a good model
for the system. |
| Safety
Issues |
Air track motors can overheat if the air
inlet is blocked. |
| Equipment
Limitations |
Air tracks an their sliders are much more
delicate than they look. Do NOT drop or strike them |
| Resources/Materials: |
Air track and slider, photogates, computer system set up with
Vernier LabPro software and Lab Pro units |
|